力扣题型提示
1.单调队列
1.单调队列
1.偏差与方差


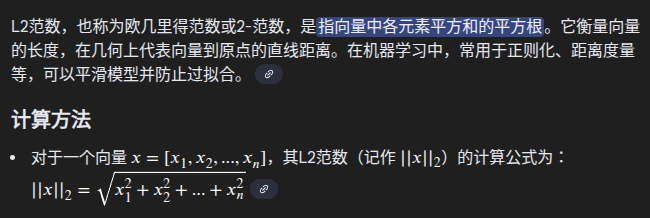
2.L2范数
Frenet坐标系:[$s$,$\dot{s}$,$\ddot{s}$,l,$\dot{l}$,$\ddot{l}$,${l}'$,${l}''$]
Cartesian坐标系:[$\vec{x} $,$v_{x}$,$a_{x}$,$\theta_{x}$,$k_{x}$]
$s$:Frenet纵坐标
$\dot{s}$=$\frac{ds}{dt} $:Frenet纵坐标对时间的导数,纵向速度
$\ddot{s}$=$\frac{\dot{ds}}{dt} $:纵向加速度
$l$:Frenet横坐标
$\dot{l}$=$\frac{dl}{dt}$:Frenet横向速度
$\ddot{l}$=$\frac{d\dot{l}}{dt}$:Frenet横向加速度
${l}'$=$\frac{dl}{ds}$:Frenet横向坐标对纵向坐标的导数
${l}''$=$\frac{\dot{dl}}{ds}$:Frenet横向坐标对纵向坐标的二阶导
$\vec{x} $:Cartesian坐标系下的一个向量
$\theta_{x}$:Cartesian坐标系下的朝向
$k_{x}$=$\frac{d{\theta_{x}}}{ds}$:曲率
$v_{x}$=$\left \| \dot{\vec{x} } \right \| _{2}$:Cartesian坐标系下的线速度
$a_{x}$=$\frac{dv_{x}}{dt}$:Cartesian坐标系下的加速度
推导过程:
真因数:除了x本身,x的所有正因数 质数:是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。 质数的平方恰好有两个真因数


